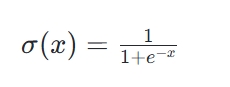Sigmoid函数是一种数学函数，具有特征“S”形曲线或S形曲线，通常指的是逻辑函数的特殊情况。它在生物学、信息科学、神经网络等多个领域广泛应用。Sigmoid函数的一个常见例子是logistic函数，其公式为：
Sigmoid函数的主要特点包括：
- 单调递增：函数在整个定义域内单调递增。
- 对称性：函数在(0, 0.5)处对称。
- 输出范围：函数的输出值在0到1之间，这使得它非常适合用于表示概率。
- 非线性：Sigmoid函数引入了非线性，使得神经网络能够学习更复杂的决策边界。
- 可微性：函数是可微的，这使得它可以用于梯度下降等优化算法中。
在神经网络中，Sigmoid函数常被用作激活函数，特别是在前馈神经网络中。它的作用是将输入值映射到0和1之间，从而将神经元的输出进行归一化处理。
然而，Sigmoid函数也存在一些缺点：
- 梯度消失问题：在输入值较大或较小时，Sigmoid函数的导数接近于0，这会导致梯度消失问题，影响模型的训练效果。
- 输出范围限制：虽然输出范围在0到1之间，但在某些情况下，这种限制可能会影响模型的性能。
Sigmoid函数是一种常用的激活函数，具有单调递增、对称性、输出范围有限等优点，但也存在梯度消失和输出范围限制等缺点。在实际应用中，需要根据具体问题选择合适的激活函数
声明：文章来源于网络，如有侵权请联系删除！