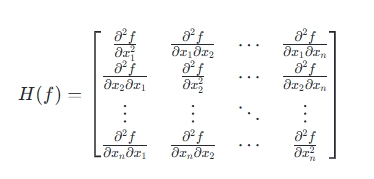Hessian矩阵是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。具体来说,对于一个函数 f(x1,x2,…,xn),如果所有的二阶导数都存在,那么它的Hessian矩阵定义为:
Hessian矩阵具有以下性质:
- 对称性:Hessian矩阵是对称的,即 Hij=Hji。
- 应用:Hessian矩阵在优化问题中有着广泛的应用,例如判断函数是否有最小值。Hessian矩阵正定是函数存在最小值的充分条件。
Hessian矩阵在图像处理、机器学习、优化算法等领域也有重要应用。例如,在图像处理中,Hessian矩阵用于边缘检测和纹理分析;在机器学习中,Hessian矩阵用于牛顿法最优化算法和XGBoost算法中。
Hessian矩阵是理解函数在特定点附近行为的关键工具,尤其是在处理多变量函数的高阶导数时。通过Hessian矩阵,我们可以更好地掌握函数的性质,并找到更准确的近似值。
声明:文章均为AI生成,请谨慎辨别信息的真伪和可靠性!