什么是FP8矩阵乘法

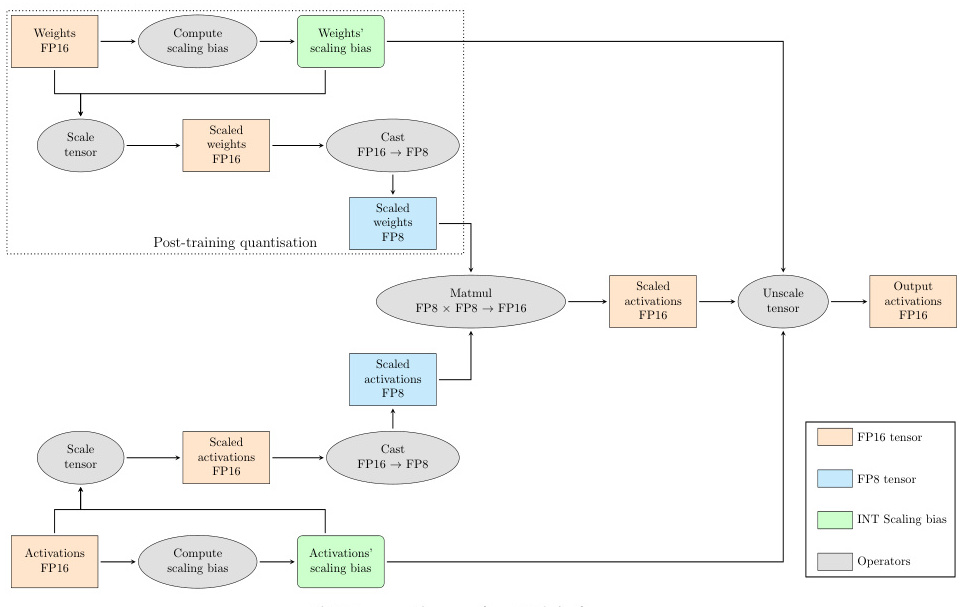
FP8矩阵乘法是一种利用8位浮点数（FP8）进行矩阵运算的技术，旨在通过减少数据类型所需的比特数来提高计算效率和内存利用率，同时尽量保持计算精度。FP8矩阵乘法在深度学习模型的训练和推理中具有重要作用，特别是在大规模模型和高性能计算场景中。

FP8矩阵乘法的基本概念

1. FP8数据类型：
   • FP8是一种8位浮点数表示法，分为E4M3和E5M2两种格式，分别对应不同的指数和尾数位数。
   • E4M3格式具有较小的动态范围，而E5M2格式则提供了更大的动态范围。
   • FP8数据类型占用的比特数比FP16少一半，但比INT8多，因此在精度和内存占用之间取得了一定的平衡。
2. 计算性能：
   • FP8矩阵乘法利用Tensor Core单元进行加速，Tensor Core专为矩阵乘法和累积（MMA）操作设计，能够在单个时钟周期内完成多次矩阵乘法和加法运算。
   • 在NVIDIA Hopper架构中，Tensor Core单元的并行计算能力显著提高了FP8矩阵乘法的效率。
3. 应用场景：
   • FP8矩阵乘法广泛应用于Transformer模型、图像分类、目标检测、自然语言处理等领域。
   • 在大规模分布式训练系统中，FP8矩阵乘法可以显著加速GEMM（General Matrix Multiplication）操作。

实现细节

1. 量化与反量化：
   • 在FP8矩阵乘法中，输入数据通常先从FP16或FP32量化为FP8格式，计算完成后将结果反量化回FP16或FP32格式。
   • 量化过程包括计算缩放因子（scale factor），并根据缩放因子将数据转换为FP8格式。

2. 动态量化：

• 动态量化是在运行时将FP16激活量化为FP8格式，并使用Triton FP8进行矩阵乘法运算。
• 动态量化可以显著减少内存占用，同时保持较高的计算性能。

3. 持久化内核：
   • 持久化内核（Persistent Kernel）是一种优化技术，通过将矩阵乘法操作分解为多个小块并行处理，进一步提高计算效率。
4. API支持：
   • cuBLAS廖库提供了原生计算FP8矩阵乘法的公式和相关函数，如cublasLtMatmul()和cublasLtMatmulDescAttributes_t。
   • 用户可以通过设置环境变量或调用API来禁用某些CPU指令，以优化FP8矩阵乘法的性能。

性能优化

1. 内存优化：
   • FP8矩阵乘法通过减少数据类型所需的比特数，显著降低了内存占用，特别是在处理大规模模型时。
   • 在Transformer模型中，使用FP8矩阵乘法可以减少显存占用，从而支持更大的模型。
2. 精度控制：
   • 尽管FP8矩阵乘法的动态范围有限，但通过合理选择指数位数和尾数位数，可以在精度和效率之间取得平衡。
   • 在某些情况下，可以通过分块累加和高精度累加器来防止下溢现象。
3. 硬件支持：
   • NVIDIA Hopper架构和Ada Lovelace架构的GPU支持FP8矩阵乘法，提供了更高的计算效率和更低的内存占用。
   • AMD GPU也支持FP8矩阵乘法，进一步扩展了其应用范围。

总结

FP8矩阵乘法是一种高效的数据类型转换技术，通过减少数据类型所需的比特数来提高计算效率和内存利用率。它在深度学习模型的训练和推理中具有广泛的应用前景，特别是在大规模模型和高性能计算场景中。通过合理的量化与反量化策略、持久化内核优化以及硬件支持，FP8矩阵乘法能够在保持较高精度的同时，显著提升计算性能和内存效率。