什么是FP16矩阵乘法

FP16矩阵乘法是指使用半精度浮点数（FP16）进行矩阵乘法运算的技术。FP16是一种16位浮点数格式，相比于传统的32位浮点数（FP32）和64位浮点数（FP64），FP16具有更高的计算效率和更低的内存占用，但精度较低。

FP16矩阵乘法的特点和应用场景

1. 计算效率：
   • FP16矩阵乘法可以在GPU上高效执行，显著提高计算速度。例如，在NVIDIA的Tensor Core架构中，FP16矩阵乘法可以达到每秒数十TFLOPS的性能。
   • 在某些情况下，FP16矩阵乘法的速度甚至可以与FP32矩阵乘法相媲美，尤其是在特定的硬件优化下。
2. 内存占用：
   • FP16矩阵乘法所需的显存是FP32的四分之一，这使得在内存资源有限的情况下，FP16成为一种有效的选择。
   • 然而，FP16的精度较低，可能会导致数值稳定性问题，因此在某些需要高精度的场景中，仍需使用FP32或更高精度的格式。
3. 精度权衡：
   • FP16矩阵乘法在精度上不如FP32，但在许多深度学习任务中，通过梯度更新和反向传播，FP16的精度损失可以被有效控制。
   • 在推理阶段，FP16矩阵乘法通常能够提供与FP32相近的精度，尤其是在现代硬件的支持下。
4. 硬件支持：
   • 现代GPU（如NVIDIA的Volta、Turing和Ampere架构）提供了对FP16矩阵乘法的硬件支持，显著提高了计算效率。
   • 在一些特定的硬件架构中，如Intel的Xe GPU和Qualcomm的NPU，也支持FP16矩阵乘法。
5. 应用场景：
   • FP16矩阵乘法广泛应用于深度学习模型的训练和推理中，特别是在大规模模型和高性能计算场景中。
   • 在自然语言处理（NLP）和计算机视觉任务中，FP16矩阵乘法被用于加速模型的训练和推理过程。

实现方法

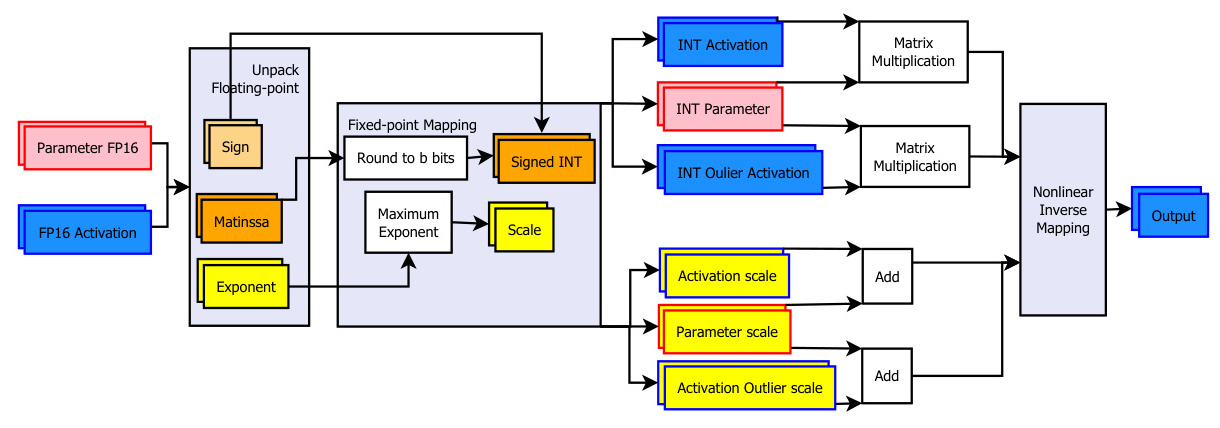
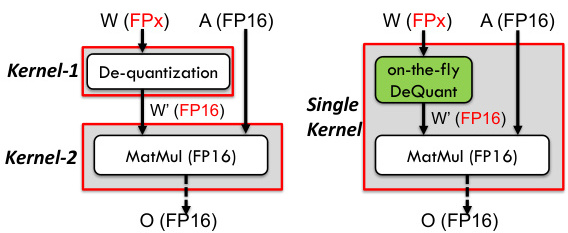
1. 量化和去量化：
   • 在进行FP16矩阵乘法之前，通常需要将输入数据从更高精度（如FP32）量化为FP16格式。量化过程中会提取指数、尾数和符号位，并将其转换为FP16格式。
   • 在计算完成后，需要将结果从FP16反量化回更高精度（如FP32），以确保最终结果的精度。

2. 混合精度训练：

• 在混合精度训练中，FP16矩阵乘法通常用于前向传播和后向传播中的某些步骤，而关键操作（如梯度更新）则使用更高精度（如FP32）进行。

3. 优化算法：
   • 为了提高FP16矩阵乘法的性能，研究者们提出了多种优化算法，如块级矩阵乘法、多维指针算术和程序重排序等。
   • 这些优化方法可以显著提高FP16矩阵乘法的计算效率和缓存利用率。

总结

FP16矩阵乘法是一种高效且低资源消耗的矩阵运算技术，广泛应用于深度学习模型的训练和推理中。尽管其精度较低，但在现代硬件的支持下，通过量化和去量化、混合精度训练以及优化算法，FP16矩阵乘法可以在保持较高精度的同时显著提高计算效率。