什么是非负矩阵分解（NMF）

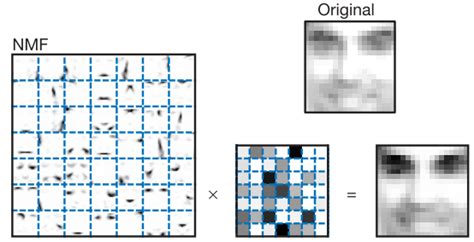
非负矩阵分解（Non-negative Matrix Factorization，NMF）是一种矩阵分解方法，其核心思想是将一个非负矩阵分解为两个或多个非负矩阵的乘积。这种方法最初由D.D.Lee和H.S-Seung在1999年提出，并广泛应用于数据降维、特征提取、模式识别等领域。

基本原理

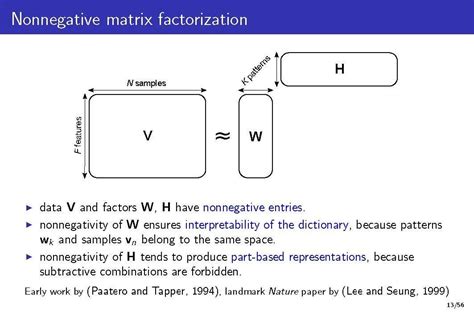
非负矩阵分解的目标是将一个非负矩阵 $A$ 分解为两个非负矩阵 $W$ 和 H，使得它们的乘积 WH 能够近似原始矩阵 $A$。数学上可以表示为：
A≈WH

其中，W 是一个 m×k 的矩阵，H 是一个 k×n 的矩阵，k 是小于 m 和 n 的整数，代表数据潜在特征的数量。

非负矩阵分解的最新进展

应用领域

NMF在多个领域有广泛应用，包括但不限于：

1. 图像处理：用于图像去噪、图像分割等。
2. 文本挖掘：用于文本聚类、主题模型等。
3. 推荐系统：用于用户行为分析和推荐算法。
4. 生物信息学：用于基因表达数据分析。
5. 信号处理：用于音频信号的分解和重构。
   

   非负矩阵分解(non-negative matrix factorization)应用于图像处理的原理及

特点与优势

1. 非负性约束：NMF要求分解后的矩阵元素均为非负值，这使得其在处理实际数据时具有直观的物理意义，例如图像像素值或文本词频等。
2. 降维与稀疏性：通过低秩近似，NMF能够有效地降低数据的维度，并且由于非负性限制，分解结果具有一定的稀疏性，这有助于揭示数据中的隐含结构。
3. 计算效率：相较于其他线性降维方法如PCA，NMF通常收敛速度更快，且更适合处理大规模数据。

实现方法

NMF的实现通常依赖于迭代优化算法，如梯度下降法、乘法更新规则等。这些算法的目标是最小化重构误差，常用的损失函数包括Frobenius范数、KL散度等。

机器学习：非负矩阵分解（NMF）_非负矩阵分解算法的优化算法

总结

非负矩阵分解是一种强大的数据处理工具，尤其适用于处理非负数据。它通过将高维数据映射到低维空间，揭示数据的内在结构和模式，从而在多个领域中发挥重要作用。NMF不仅在理论上具有重要意义，而且在实际应用中也展现了广泛的应用潜力