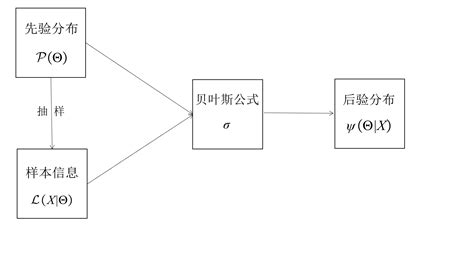
贝叶斯估计是一种统计推断方法,通过结合先验分布和观测数据来估计未知参数。其核心思想是利用贝叶斯定理,将先验知识与新数据结合起来,从而得到后验分布,进而计算参数的估计值。
贝叶斯估计的基本原理
- 先验分布:在进行估计之前,我们对参数的分布有一定的先验知识,这通常以概率分布的形式表示。例如,我们可能认为某个参数服从正态分布或均匀分布。
- 似然函数:基于观测数据,我们计算参数的似然函数,即在给定参数值的情况下,观测数据出现的概率。
- 后验分布:通过贝叶斯定理,将先验分布和似然函数结合起来,得到参数的后验分布。后验分布反映了在观测数据的基础上对参数的新认识。
- 估计量的选择:根据后验分布,可以选择不同的估计量,如后验均值、中位数或模式等。这些估计量的选择取决于具体的损失函数和应用场景。
贝叶斯估计的步骤
- 确定先验分布:选择一个合理的先验分布,这通常基于领域知识或经验。
- 计算似然函数:根据观测数据,计算参数的似然函数。
- 计算后验分布:通过贝叶斯定理,结合先验分布和似然函数,得到参数的后验分布。
- 选择估计量:根据后验分布,选择一个合适的估计量(如后验均值、中位数或模式)。
贝叶斯估计的特点
- 灵活性:贝叶斯估计允许在估计过程中引入先验知识,这在数据量较少或模型复杂时尤为重要。
- 不确定性量化:贝叶斯估计不仅提供参数的估计值,还提供了参数的不确定性范围(如置信区间),这有助于更全面地理解结果。
- 适用性广泛:贝叶斯估计可以应用于各种统计模型和领域,如医学、金融、工程等。
贝叶斯估计的应用
- 分类器设计:在机器学习中,贝叶斯估计可以用于分类器的设计,通过最大化后验期望值来选择最优分类器。
- 回归分析:在回归分析中,贝叶斯估计可以用于估计回归系数,并提供其不确定性范围。
- 信号处理:在信号处理中,贝叶斯估计可以用于递归地估计未知的概率密度函数。
- 工程设计:在工程设计中,贝叶斯估计可以用于优化设计参数,提高设计的可靠性和效率。
贝叶斯估计的局限性
- 先验分布的选择:先验分布的选择对结果有较大影响,如果先验分布不准确,可能导致估计结果偏差。
- 计算复杂性:在某些情况下,后验分布可能难以解析表达,需要借助数值方法进行计算。
- 依赖于数据:贝叶斯估计的结果高度依赖于观测数据的质量和数量。
贝叶斯估计是一种强大的统计推断方法,通过结合先验知识和观测数据,能够提供更全面和可靠的参数估计。然而,在实际应用中,需要仔细选择先验分布并考虑计算复杂性。
声明:文章均为AI生成,请谨慎辨别信息的真伪和可靠性!