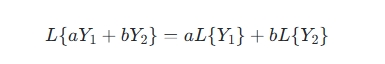线性滤波技术是一种通过对输入信号进行线性变换来实现滤波功能的技术。其核心思想是将输入信号的各个成分进行加权求和,从而生成输出信号。这种技术在信号处理、图像处理等领域有广泛应用。
线性滤波的基本概念
- 定义:线性滤波器是一种满足线性和齐次性条件的滤波器,即对于任何常数 a 和两个过程 Y1 和 Y2,有:
这表明线性滤波器对输入信号的加权和操作是线性的。
- 性质:
- 叠加原理:多个输入信号的线性组合经过滤波器后,其输出等于各输入信号经过滤波器后的线性组合。
- 时不变性:大多数线性滤波器具有时不变性,即滤波器对输入信号的时间平移不会导致输出信号的时间平移。
- 应用:
线性滤波器的类型
- 均值滤波器:通过计算邻域像素的平均值来平滑图像,常用于去除随机噪声。
- 高斯滤波器:使用高斯函数对邻域像素进行加权平均,能够有效消除高斯噪声,同时保留边缘信息。
- 方框滤波器:通过计算邻域像素的平均值来平滑图像,简单但可能模糊边缘。
- Sobel算子和Laplacian算子:用于边缘检测和梯度计算。
线性滤波器的设计与实现
- 卷积操作:线性滤波器通常通过卷积操作实现,即将滤波器核(或卷积核)与输入信号进行卷积运算。
- 滤波器核:滤波器核定义了对输入信号的加权方式,常见的核包括均值核、高斯核等。
- 实现工具:可以使用MATLAB、OpenCV等工具实现线性滤波功能。
线性滤波器的特点
- 可控性强:通过调整滤波器核的权重,可以灵活实现不同的滤波效果。
- 易于实现:算法相对简单,适合实时信号处理和嵌入式系统。
- 局限性:只能处理线性系统下的信号,对于非线性和非线性系统效果可能不佳。
线性滤波器的应用实例
- 图像去噪:通过高斯滤波器去除图像中的高斯噪声。
- 边缘检测:使用Sobel算子或Laplacian算子提取图像边缘。
- 信号平滑:通过均值滤波器平滑时间序列数据。
线性滤波技术是一种重要的信号处理工具,广泛应用于信号处理和图像处理领域。其核心在于通过对输入信号进行线性加权求和来实现滤波功能,具有可控性强、易于实现等特点,但也存在一定的局限性。
声明:文章均为AI生成,请谨慎辨别信息的真伪和可靠性!