直方图是一种用于展示数据分布情况的统计图表,通过一系列矩形的宽度和高度来表示数据在不同区间内的频率或数量。直方图主要用于展示连续型变量的分布情况,其横轴表示数据的范围,纵轴表示频率或相对频率。
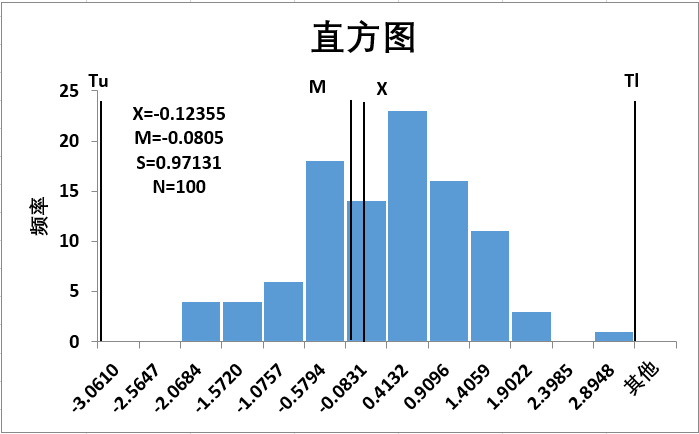
直方图的基本构成
- 横轴:表示数据的范围或类别。
- 纵轴:表示频率(实际频数)或相对频率(频数除以总频数)。
- 矩形:每个矩形代表一个数据区间,矩形的高度表示该区间内的数据频率或相对频率。
直方图的特点
- 连续性:直方图适用于连续型变量,各组之间没有间隙。
- 频率表示:直方图通过矩形的高度来表示数据在各个区间内的频率。
- 等宽分组:通常情况下,直方图的区间是等宽的,但也可以根据需要调整区间宽度。
直方图的类型
- 基本直方图:展示每个区间的频率分布。
- 累积直方图:展示累计频率,即所有小于等于某个区间的频率总和。
- 相对频率直方图:纵轴表示相对频率,即每个区间的频率除以总频数。
- 正态分布直方图:如果数据符合正态分布,直方图会呈现出钟形曲线。
直方图的应用
- 数据分析:通过直方图可以快速识别数据的分布形状、集中趋势和异常值。
- 质量控制:在生产过程中,直方图可以用来监控产品质量,判断生产过程是否稳定。
- 图像处理:在图像处理中,直方图用于分析图像的亮度分布,帮助调整图像的对比度和亮度。
直方图的制作步骤
- 确定数据范围:将数据划分为若干个区间(bin)。
- 计算频率:统计每个区间内的数据点数量。
- 绘制直方图:根据计算结果绘制矩形,矩形的高度表示该区间的频率或相对频率。
直方图的优缺点
- 优点:
- 直观性强,能够清晰地展示数据的分布情况。
- 适用于连续型变量,能够有效展示数据的集中趋势和离散程度。
- 缺点:
- 区间宽度的选择会影响直方图的外观和解释,过宽或过窄的区间可能导致信息丢失或误导。
- 不适合离散型变量,因为离散型变量之间需要有间隙。
直方图的软件工具
- Python:可以使用Matplotlib库中的
hist()函数绘制直方图。 - Excel:可以通过内置的图表功能创建直方图。
- R语言:可以使用ggplot2包绘制直方图。
示例
假设我们有一组学生的考试成绩数据,范围从0到100。我们可以将成绩分为10个区间(例如,0-9, 10-19, ..., 90-99, 100),然后统计每个区间内的学生人数。绘制出的直方图将显示每个区间的学生人数分布情况。
直方图是一种强大的统计工具,广泛应用于科学研究、数据分析、质量控制等领域。通过合理选择区间宽度和解释直方图的形状,可以有效地揭示数据的分布特征和潜在规律
声明:文章均为AI生成,请谨慎辨别信息的真伪和可靠性!

