什么是正则化项（regularization term）

正则化项（Regularization Term）是机器学习和数学优化中的一种技术，用于防止模型过拟合，提高模型的泛化能力。其核心思想是在损失函数中加入一个额外的惩罚项，通过约束模型的复杂度来避免模型对训练数据的过度拟合。正则化项通常位于损失函数之后，以控制模型的结构风险，从而平衡经验风险（模型在训练数据上的表现）和模型复杂度。

正则化项的作用

1. 防止过拟合：正则化项通过限制模型的复杂度，避免模型对训练数据中的噪声或偶然特征进行学习，从而提升模型在未见数据上的表现。
2. 控制模型复杂度：正则化项可以限制模型参数的大小或稀疏性，使模型更加简单，从而减少过拟合的风险。
3. 特征选择和稀疏性：某些正则化形式（如L1正则化）可以通过将部分参数设置为零来实现特征选择，而L2正则化则通过惩罚参数的平方和来实现稀疏性。

正则化项的常见形式

1. L1正则化（Lasso） ：通过惩罚参数的绝对值之和来实现稀疏性，部分参数可能被精确地设置为零，从而实现特征选择。
   
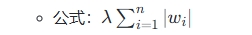
2. L2正则化（Ridge） ：通过惩罚参数的平方和来实现平滑性，所有参数不会被精确地设置为零。
   
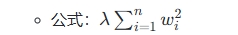
3. 结合L1和L2正则化：同时使用L1和L2正则化，结合了稀疏性和平滑性的优点，称为Elastic Net。
4. 其他形式：如核范数正则化、Tikhonov正则化等，用于特定问题的优化。

正则化项的应用场景

1. 深度学习：在神经网络中，正则化项常用于权重矩阵的惩罚，以防止过拟合并提高模型的泛化能力。
2. 图像处理：在图像恢复和分割任务中，正则化项用于优化目标函数，以提高图像的质量和清晰度。
3. 半监督学习：在无标签数据较多的情况下，正则化项可以用于惩罚标签分配的不一致性。

正则化项的选择

选择合适的正则化项需要根据具体问题和数据特性进行调整。例如：

• 当需要稀疏模型时，选择L1正则化；
• 当需要平滑模型时，选择L2正则化；
• 当需要同时考虑稀疏性和平滑性时，选择Elastic Net。

正则化项是机器学习和优化问题中不可或缺的技术，通过合理设计和调整正则化项，可以显著提升模型的性能和泛化能力。