什么是正交矩阵（Orthogonal Matrix）

正交矩阵（Orthogonal Matrix）是线性代数中的一个重要概念，具有许多独特的性质和广泛的应用。以下是对正交矩阵的详细解释：

定义

正交矩阵是指满足以下条件的 n×n实数矩阵 Q：

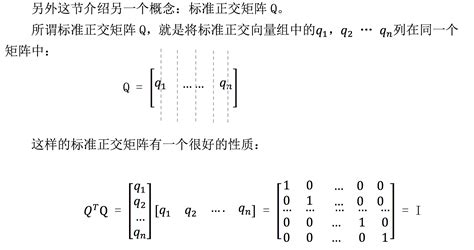
1. QTQ=1，其中 QT 是 Q 的转置矩阵，1是单位矩阵。
2. 等价地，Q−1=QT，即 Q 的逆矩阵等于其转置矩阵。
3. 正交矩阵的行列式值为 ±1。

正交矩阵和 Gram-Schmidt 正交化(MIT线代第十七课) - 知乎

性质

1. 单位向量：正交矩阵的每一行和每一列都是单位向量，且两两正交。
2. 保持向量长度和角度：正交矩阵在进行线性变换时，保持向量的长度和夹角不变。这意味着，如果 x 和 y 是两个向量，则有 ∥Ax∥=∥x∥ 和 ⟨Ax,Ay⟩=⟨x,y⟩。
3. 逆矩阵和转置矩阵：正交矩阵的逆矩阵和转置矩阵是相同的，即 Q−1=QT。
4. 行列式：正交矩阵的行列式值为 ±1，这表明其体积不变性。
5. 正交变换：正交矩阵对应的变换称为正交变换，这种变换在几何中表现为旋转或反射。
6. 特征值：正交矩阵的特征值的模长为 1，即所有特征值的绝对值均为 1。

什么是正交矩阵

应用

正交矩阵在多个领域中有着重要的应用：

1. 线性代数：正交矩阵在矩阵分解、特征值分析等方面具有重要作用。
2. 计算机图形学：正交矩阵用于实现三维空间中的旋转和平移操作。
3. 信号处理：在信号处理中，正交矩阵用于滤波器设计和信号分解。
4. 物理学：在物理学中，正交矩阵用于描述旋转和反射等对称性。

示例

总结

正交矩阵是一种特殊的方阵，其行和列向量均为单位向量且两两正交。它在数学、物理和工程等多个领域中具有广泛的应用，因其保持向量长度和角度不变的特性而备受重视。理解正交矩阵的定义和性质对于深入学习线性代数及其应用至关重要