什么是梯度下降（Gradient Descent）

梯度下降（Gradient Descent）是一种在机器学习和优化问题中广泛使用的迭代优化算法，其核心目标是通过调整参数来最小化损失函数或目标函数的值。以下是梯度下降的详细解释：

1. 基本原理

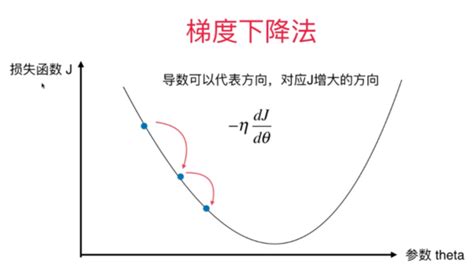
梯度下降的基本思想是利用函数的梯度信息（即导数）来更新参数，从而逐步接近损失函数的最小值。梯度表示函数在某一点处的变化方向和大小，通常用向量形式表示。在数学上，梯度是损失函数关于参数的一阶导数，指向函数增长最快的方向。因此，沿着梯度的反方向移动可以更快地接近最小值。

梯度下降

2. 算法步骤

梯度下降算法的步骤如下：

1. 初始化参数：随机选择一个初始参数值。
2. 计算梯度：计算损失函数关于当前参数的梯度。
3. 更新参数：根据学习率（步长）和梯度更新参数。
4. 重复迭代：直到满足停止条件（如梯度接近零或达到最大迭代次数）。

梯度下降的数学公式：

梯度下降的三要素

1. 当前点；
2. 方向；
3. 步长。

3. 变种

梯度下降有多种变种，每种变种在计算效率和稳定性上有所不同：

1. 批量梯度下降（Batch Gradient Descent） ：使用所有训练数据计算梯度，适用于数据量较小的情况。
2. 随机梯度下降（Stochastic Gradient Descent, SGD） ：每次迭代只使用一个样本计算梯度，适用于大规模数据集，但可能收敛速度较慢。
3. 小批量梯度下降（Mini-batch Gradient Descent） ：每次迭代使用一小部分样本计算梯度，结合了批量梯度下降和随机梯度下降的优点，是深度学习中最常用的优化方法。
   

   三种梯度下降算法的实现——批量梯度下降，随 …

4. 关键参数

• 学习率（Learning Rate） ：控制每次更新的步长。如果学习率过大，可能导致震荡或发散；如果过小，则收敛速度慢。
• 收敛条件：通常通过判断梯度的大小或损失函数的变化幅度来决定是否停止迭代。

5. 应用场景

梯度下降广泛应用于各种机器学习任务中，包括：

• 线性回归和逻辑回归
• 神经网络训练
• 非线性方程求解。

6. 优缺点

优点：

• 算法简单且易于实现。
• 可以处理复杂的非凸优化问题。
• 学习率调整策略（如学习率衰减）可以提高收敛速度。

缺点：

• 只能找到局部最小值，无法保证全局最优。
• 对于高维数据或复杂模型，计算成本较高。
• 学习率的选择对收敛速度和稳定性有重要影响。

7. 实际应用示例

在神经网络中，梯度下降用于更新权重参数，以最小化预测输出与实际输出之间的误差。通过反向传播算法计算损失函数的梯度，并结合学习率逐步调整权重。

8. 总结

梯度下降是一种强大的优化算法，通过迭代调整参数来最小化损失函数。其变种（如SGD和Mini-batch GD）进一步提高了算法的适用性和效率。理解梯度下降的原理和实现方法对于掌握机器学习和深度学习至关重要

9、相关来源链接：

02.3 梯度下降 - AI-EDU