什么是核密度估计（Kernel Density Estimation，KDE）

核密度估计（Kernel Density Estimation，KDE）是一种非参数统计方法，用于估计未知随机变量的概率密度函数（PDF）。它通过在每个数据点周围放置一个核函数，并对所有核函数的值进行加权平均来估计概率密度。这种方法不依赖于任何特定的分布假设，因此在处理复杂或非线性分布时具有较大的灵活性。

核密度估计的基本原理

1. 核函数：核函数是一个对称的、非负的函数，通常满足积分等于1的条件。常见的核函数包括高斯核、Epanechnikov核、三角核等。核函数的选择对估计结果有重要影响，不同的核函数可以捕捉数据的不同特征。
2. 带宽参数：带宽参数 $h$ 是核密度估计中的一个关键超参数，决定了核函数的宽度。带宽的选择对估计结果有显著影响：
   • 较小的带宽会导致估计结果过于波动，容易受到噪声的影响。
   • 较大的带宽则会使估计结果过于平滑，可能掩盖数据的局部特征。
3. 估计公式：核密度估计的公式为：

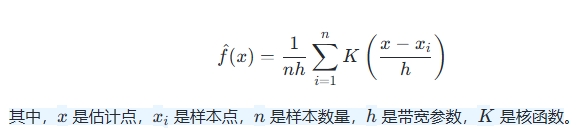
核密度估计的应用

1. 数据可视化：KDE 可以用于绘制数据的平滑分布图，帮助理解数据的分布特性。例如，在金融领域，可以使用 KDE 绘制股票收益率的分布图。
2. 异常检测：通过 KDE 生成的概率密度图，可以识别出数据中的异常值。例如，在网络安全领域，可以检测网络流量中的异常活动。
3. 模式识别：KDE 可以用于模式识别任务，如分类和聚类。通过估计不同类别的概率密度，可以更好地理解数据的分布特征。
4. 高维数据分析：KDE 也可以扩展到多维数据，通过双变量或更高维度的核函数来估计高维数据的密度分布。

核密度估计的优势

1. 非参数性：KDE 不需要对数据分布做任何假设，适用于各种复杂分布。
2. 灵活性：通过选择不同的核函数和带宽参数，可以适应不同的数据特征。
3. 鲁棒性：KDE 对于小样本数据也能提供较为准确的估计。

核密度估计的局限性

1. 计算量大：对于大规模数据集，KDE 的计算成本较高，尤其是在高维数据情况下。
2. 带宽选择敏感：带宽的选择对估计结果有显著影响，选择不当可能导致估计结果失真。

实现方法

在实际应用中，可以使用多种编程语言和库来实现 KDE。例如，在 Python 中，可以使用 scipy.stats.gaussian_kde 或 seaborn 库中的 kdeplot 函数来绘制 KDE 图。

核密度估计是一种强大的统计工具，广泛应用于数据可视化、异常检测、模式识别等领域。通过合理选择核函数和带宽参数，可以有效地估计数据的分布特征。