数值积分技术是一种通过数值方法近似计算定积分值的技术，主要用于解决函数解析表达式未知或积分计算过于复杂的情况。其核心思想是将积分区间划分为若干小区间，并在每个小区间上用近似函数（如多项式）来代替被积函数，然后通过求和的方式得到积分的近似值。
数值积分的基本概念
数值积分的基本思想是将积分区间划分为若干小区间，然后在每个小区间上用近似函数代替被积函数，最后通过求和的方式得到积分的近似值。这种方法不需要被积函数的解析表达式，只需知道其在某些点上的值即可。数值积分技术广泛应用于工程、物理、金融等领域，用于计算曲线长度、流体动力学、经济指标等。
常见的数值积分技术
以下是几种常见的数值积分方法及其特点：
- 矩形法
矩形法是最简单的数值积分方法，将积分区间划分为若干小区间，在每个小区间上用矩形面积近似被积函数的值。矩形法精度较低，适用于简单函数的积分计算。
矩形法_矩形重叠-CSDN博客 - 梯形法
梯形法通过连接小区间的端点形成梯形，用梯形面积近似被积函数的值。相比矩形法，梯形法精度更高，但仍然属于低阶方法。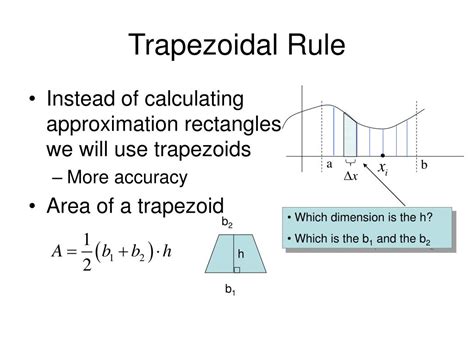
PPT - CHAPTER 4 SECTION 4.6 NUMERICAL INTEGRATION PowerPoint ... - 辛普森法
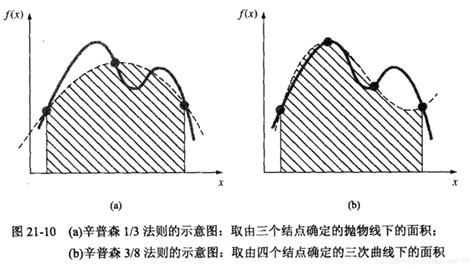
辛普森法使用二次多项式近似被积函数，通过抛物线连接相邻三个点来计算积分值。辛普森法精度较高，适用于平滑函数的积分计算。
数值积分方法的总结（从简单梯形积分到龙贝格积分、自适应积分、高斯积分等） - 高斯求积法
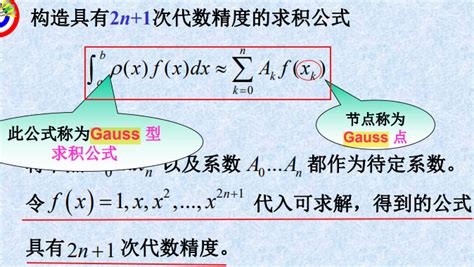
高斯求积法通过选择特定的节点（称为高斯点）并应用加权和来近似积分值。该方法精度高，计算速度快，但需要确定节点和权重。高斯求积法特别适用于需要高精度计算的场景。
利用高斯求积公式计算积分_高斯切比雪夫求积公式的推导 - 思创斯聊编程 - Romberg积分法
Romberg积分法基于梯形法，通过递归计算和外推技术提高积分精度。该方法适用于大区间上的积分计算，具有较高的精度和稳定性。
计算方法 7.数值积分计算方法_直接积分法的数值计算-CSDN博客 - 龙贝格积分法
龙贝格积分法基于Richardson外推法，逐步增加节点数以提高积分精度。该方法计算公式简洁，适用范围广。
PPT - 数值积分 PowerPoint Presentation, free download - ID:510… - 自适应积分法
自适应积分法通过动态调整步长或求值点数量来提高计算精度，同时降低计算成本。这种方法特别适用于处理不连续性、奇异性或快速振荡函数。
数值积分的应用领域
数值积分技术在多个领域中发挥着重要作用：
- 工程领域：用于结构应力分布、流体动力学中的速度场计算等。
- 物理领域：用于计算物体的运动轨迹、电磁场分布等。
- 金融领域：用于评估衍生品价值、模拟污染物扩散等。
- 科学研究：用于计算圆周率、热传导和熵等。
数值积分的优势与挑战
优势：
- 不需要被积函数的解析表达式。
- 可以快速处理复杂的积分问题。
- 在现代计算技术的支持下，可以高效地处理高维积分问题。
挑战：
- 对于某些复杂函数，可能需要较高的计算资源。
- 高精度计算可能需要复杂的节点选择和权重计算。
结论
数值积分技术是数学分析的重要工具，广泛应用于科学研究和工程实践中。通过合理选择数值积分方法，可以有效提高计算效率和精度，解决实际问题中的复杂积分问题
声明：文章均为AI生成，请谨慎辨别信息的真伪和可靠性！