什么是投影矩阵

什么是投影矩阵

投影矩阵（Projection Matrix）是一种特殊的线性变换矩阵，用于描述向量在空间中的投影变换，它具有以下几个关键性质：

1. 幂等性：投影矩阵满足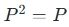，即对自身进行两次变换与一次变换结果相同。这一性质表明投影矩阵在多次应用时不会改变结果，保持了投影的稳定性。
2. 对称性：投影矩阵是对称矩阵，即 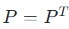。这意味着投影矩阵的行和列是互为转置的，反映了投影操作的对称性。
3. 正交性：在某些情况下，投影矩阵还具有正交性，即 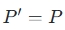，这表明投影矩阵在正交投影中保持不变。
4. 子空间投影：投影矩阵可以将一个向量投影到一个子空间或其正交补空间。这种投影操作在数学和计算机图形学中广泛应用，特别是在三维空间到二维平面的投影中。
5. 计算方法：投影矩阵的计算方法取决于具体的应用场景。例如，在计算机图形学中，透视投影矩阵和正交投影矩阵用于将3D场景渲染到2D屏幕上。
6. 特殊情况：在某些情况下，如二维和三维空间中，投影矩阵可以是单位矩阵，因为投影到自身的向量不会改变。
7. 应用领域：投影矩阵在多个领域有重要应用，包括计算机图形学中的3D到2D投影、线性代数中的向量投影、统计学中的最小二乘法等。

综上所述，投影矩阵是一种具有幂等性和对称性的特殊矩阵，用于将向量投影到特定子空间，广泛应用于数学、计算机图形学和统计学等领域。