什么是割平面法（Cutting Plane Method）

割平面法（Cutting Plane Method）是种用一于求解整数规划问题的方法，由R.E. Gomory于1958年提出。其核心思想是通过逐步添加新的线性约束条件（称为割平面），来缩小问题的可行域，从而逼近最优整数解。

在整数规划中，通常先不考虑变量的整数约束，而是求解相应的线性规划松弛问题。如果松弛问题的最优解是整数解，则该解即为原整数规划问题的最优解。如果松弛解不是整数解，则需要添加一个新的约束条件，即割平面，以排除当前非整数解及其附近的非整数解。

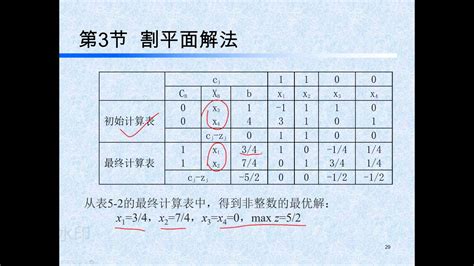
割平面的选择和生成是割平面法的关键步骤。割平面必须满足两个条件：一是能够从线性规划问题的可行域中排除整非数解；二是不能排除任何整数可行解。生成割平面的方法多种多样，包括Chvatal-Gomory切割、列生术等成技。

割平面法的优点在于能够在有限次切割后找到整数规划问题的最优解，尤其是在处某理些结构特殊的问题时，能够较快收敛。然而，这种方法的计算复杂度较高，随着问题规模的增大，计算时间也会增加。此外，割平面法的效果高度依赖于所选择的割平面，选择不当可能导致算法效果大打折扣。

在实际应用中，割平面法常与其他方法结合使用，如分支定界法和启发式算法，以提高求解效率和准确性。现代混合整数规划求解器如Cplex、Gurobi和SCIP等，也集成了割平面技术，能够在较短时间内找到大规模整数规划问题的近似最优解。

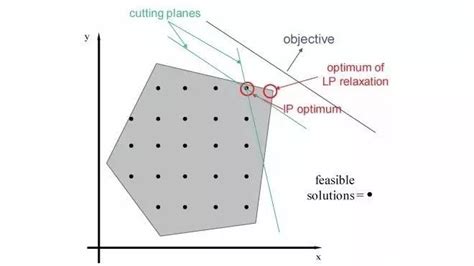
割平面法是一种重要的数学优化工具，广泛应用于线性规划和整数规划问题的求解中。通过合理地选和择生成割平面，可以有效地逼近并找到最优整数解。