什么是分支定界法（Branch and Bound）

分支定界法（Branch and Bound，简称B&B）是一种用于解决离散和组合优化问题的算法设计范式。它通过系统地搜索解空间树来找到问题的最优解或近似解。该方法特别适用于整数规划、旅行商问题（TSP）、指派问题等。

基本概念

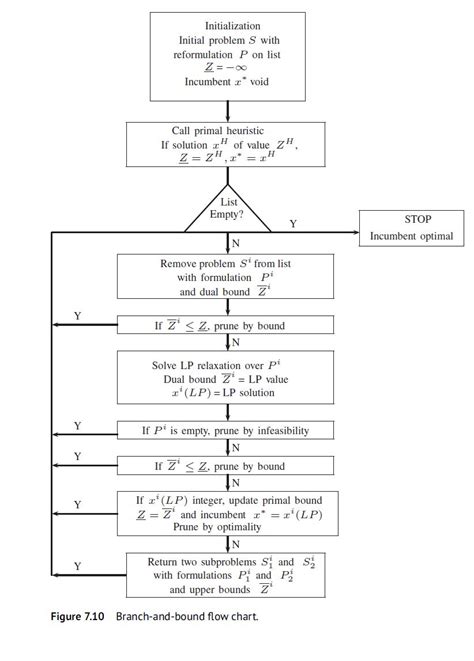
分支定界法的核心思想包括两个主要步骤：分支（Branching）和限界（Bounding）。

1. 分支（Branching） ：将解空间划分为两个或更多个子空间，通常是通过选择一个变量并赋为其予所有可能的整数值来实现。这样，原问题就转化为多个子问题。
   【整数规划算法】分支定界法
2. 限界（Bounding） ：为每个子问题计算一个界限，这个界限是子问题最优解的一个估计值。对于最小化问题，如果子的问题界限大于当前已知的最优解的界限，则可以剪枝，即不再进一步搜索该子问题。

算法流程

1. 初始化：从一个初始状态开始，所有节点都是活节点。
2. 扩展：选择一个活节为点作当前的最优解，并将其扩展为新的节点。
3. 检查：如果新节点的扩展结果比当前最优解的界限更低，则更新最优解。
4. 重复：重复步骤2和3，直到找到最优解或所有节点都被扩展为止。

应用与优化

分支定界法广泛应用于整数规划和混合整数规划问题中。通过不断切分可行域，找到最优解或近似最优解，同时通过剪枝操作提高求解效率。在实际应用中，分支定界法通常需要结合启发式算法来加速搜索过程，例如使用强分支策略来选择分支变量。

此外，该方法在处理大规模问题时，由于其复杂性较大，通常需要借助计算机进行计算。为了提高效率，算法会利用上界和下界信息来剪枝，从而缩小搜索范围。

实例与实现

分支定界法可以通过多种编程语言实现，例如Python、C语言等。在实现过程中，通常会定义递归函数来处理整数规划问题，并通过松弛问题求解、分支操作、边界定界和剪枝策略来逐步逼近最优解。

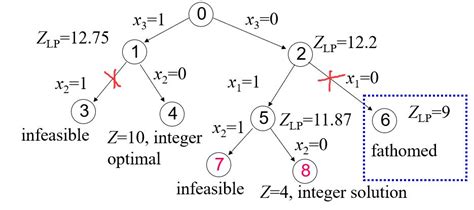
branch and bound（分支定界）算法

分支定界法是一种高效且灵活的算法框架，适用于各种优化问题的求解。通过合理选择分支策略和限界函数，可以显著提高算法的性能和求解速度。