凸优化是一种特殊的优化问题,其目标函数为凸函数,并且定义域为凸集。凸优化问题的局部最优解即为全局最优解,这使得它在求解过程中具有一定的优势。具体来说,凸优化问题可以描述为在给定的封闭凸集 C 和凸有限值函数 f 的情况下,求最小值的问题。如果 C 是紧致的且 f 是适当左极限的,则一定存在最优解;如果 f 是严格凸的,那么最小值(如果存在)是唯一的。
凸优化问题广泛应用于多个领域,包括自动控制系统、信号处理、通讯和网络、电子电路设计、数据分析和建模、统计学以及金融等。此外,凸优化在机器学习、深度学习等人工智能与大数据相关方向也有重要应用。
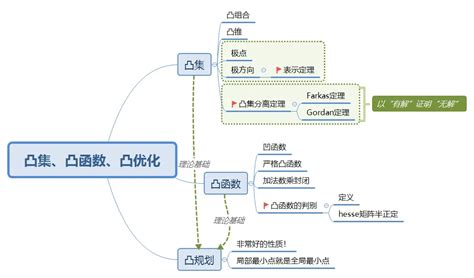
凸优化的基本概念包括凸集和凸函数。凸集是指包含任意两点之间的线段的所有点,而凸函数是指在定义域内任意两点连成的线段上的任意一点都位于该函数表示的区域内部。 凸优化问题通常可以通过改变变量或引入松弛变量来重述,从而获得更好的性质或更容易求解的问题。
总之,凸优化是一门研究如何利用凸函数的性质来解决优化问题的数学分支,具有局部最优解即全局最优解的特点,并在多个学科领域中有着广泛的应用
声明:文章均为AI生成,请谨慎辨别信息的真伪和可靠性!

