什么是低秩压缩技术

低秩压缩技术是一种通过将高维数据或矩阵分解为低秩矩阵来减少参数数量和计算复杂度的方法。其核心思想是利用数据或矩阵中的内在低秩结构，以更少的参数和计算资源近似表示原始数据，从而实现模型压缩、加速计算和降低存储需求。

低秩压缩技术的基本原理

低秩压缩技术通常通过以下步骤实现：

1. 矩阵分解：将一个高维矩阵（如权重矩阵）分解为两个或多个低秩矩阵的乘积。例如，一个矩阵 $W$ 可以被分解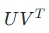为 ，其中 U 和 V 分别是 m×k 和 n×k 的矩阵，且 k≪m,n 。
2. 选择低秩：通过奇异值分解（SVD）、非负矩阵分解（NMF）或其他优化算法（如交替最小二乘法）确定合适的秩 $k$，以平衡压缩效果和模型精度 。
3. 近似与重构：通过低秩矩阵的乘积近似原始矩阵，从而减少参数数量和计算复杂度。例如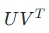，≈W。

应用领域

低秩压缩技术广泛应用于深度学习、图像处理、推荐系统等领域：

1. 深度学习：在神经网络中，低秩分解被用于压缩权重矩阵，如卷积神经网络（CNN）和循环神经网络（RNN）。通过减少参数数量，可以显著降低计算复杂度和内存占用，同时保持模型性能 。
2. 图像处理：低秩压缩技术可用于图像降噪、压缩和特征提取。例如，通过将图像矩阵分解为低秩形式，可以实现高效的图像压缩和去噪 。
3. 推荐系统：在用户-项目交互矩阵中，低秩分解可以帮助提取潜在特征，优化推荐效果 。

技术优势与挑战

优势：

1. 减少参数数量：低秩分解可以显著降低模型的参数量，从而减少存储需求和计算复杂度 。
2. 提高计算效率：通过减少参数数量，模型推理速度更快，适用于实时处理场景 。
3. 灵活性：低秩分解方法可以根据具体任务调整秩 $k$，以平衡压缩率和模型精度 。

挑战：

1. 精度损失：低秩近似可能导致模型精度下降，特别是在高维数据或复杂任务中 。
2. 计算开销：虽然低秩分解可以减少参数数量，但其本身可能需要额外的计算开销，如奇异值分解等 。
3. 选择合适的秩：如何选择合适的秩 $k$ 是一个权衡过程，需要通过实验和调优来确定最佳值 。

实现方法

常见的低秩压缩技术包括：

1. 奇异值分解（SVD） ：通过奇异值分解将矩阵分解为 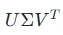，其中 Σ 包含奇异值，用于确定低秩 。
2. 非负矩阵分解（NMF） ：适用于非负数据，通过分解为两个非负矩阵来实现低秩近似 。
3. 交替最小二乘法（ALS） ：一种迭代优化算法，用于求解低秩矩阵分解问题 。
4. 张量分解：用于高维数据的低秩近似，如CP分解和Tucker分解 。

发展趋势

随着深度学习模型的不断膨胀，低秩压缩技术的应用范围和效率也在不断提升：

1. 渐进式低秩分解：逐步降低秩以提高模型精度，避免一次性降低过多秩带来的性能损失 。
2. 联合优化框架：结合损失函数和压缩成本函数，通过联合优化实现模型压缩和性能提升 。
3. 硬件适配：针对不同硬件环境设计低秩分解策略，以提高模型在实际部署中的效率 。

低秩压缩技术是一种有效的模型压缩手段，通过合理选择分解方法和参数，可以在保持模型性能的同时显著降低计算复杂度和存储需求。未来，随着算法和硬件技术的发展，低秩压缩技术有望在更多领域得到广泛应用。