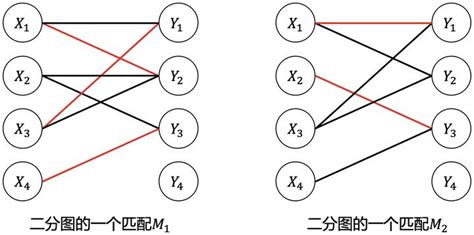
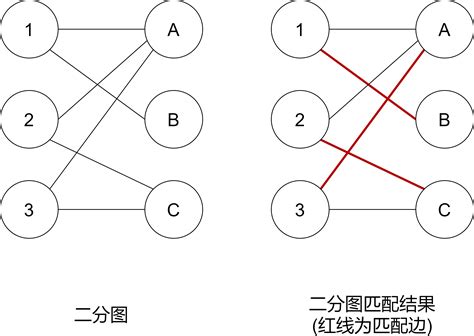
设 G=(V,E) 是一个无向图,如果顶点集 V 可以分割为两个互不相交的子集 A 和 B,使得图中的每条边 (i,j)所关联的两个顶点 i 和 j 分别属于这两个不同的子集 A 和 B,则称图 为一个二分图。
换句话说,二分图的节点可以被划分为两个集合,且这两个集合内部没有边相连,所有边都连接两个不同集合的节点。这种结构的一个重要性质是,二分图中不存在长度为奇数的环,因为任何长度为奇数的环都会导致至少一对相邻顶点属于同一个集合,这与二分图的定义相矛盾。
此外,如果一个图的所有环都是偶数长度,则该图一定是二分图。反之,如果存在奇数长度的环,则该图不能是二分图。
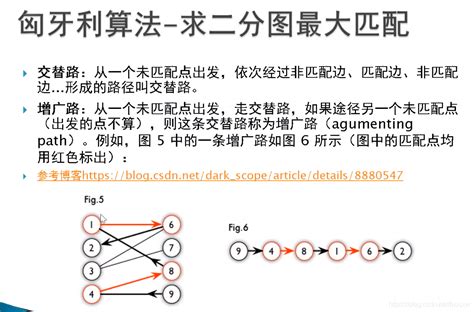
二分图在许多实际问题中有广泛应用,例如匹配问题、网络流问题等。匈牙利算法常用于求解二分图的最大匹配问题,即在二分图中找到尽可能多的边,使得这些边互不相交。
总结来说,二分图是一种特殊的无向图,其顶点可以被划分为两个互不相交的子集,且每条边连接两个不同子集的顶点。这种结构确保了图中不存在奇数长度的环,并且在许多算法和应用中具有重要地位。
声明:文章均为AI生成,请谨慎辨别信息的真伪和可靠性!